This is a bit of an unusual article, covering Suzanne, the blue monkey on our homepage.
Rendering Suzanne with Blender might not seem like something to write over 1800 words about, but there's a ton of compositing going on behind the scenes of this render and I will dive pretty deep into it here because it's quite interesting.
Why all the compositing? We're trying to maintain an accurate shadow while making the background transparent. In order to achieve this, you're just gonna need a lot of compositing nodes. Let's check it out.
Compositor walkthrough
First, here's a video of me in an attempt to walk you through the compositor chain:
In this video I'm talking about some equations I used which I translated into compositor nodes. I skipped covering the actual math because it's safe to say that the video is long enough as is 😄
So the rest of this article will just cover more of the "science" behind everything.
Shadow pixels are the actual challenge
Devoting an entire section here to Suzanne's shadow pixels. We want to get this right so I think it's necessary.
First let's get clarity on what we're trying to do. The problem is: How to get correct pixel values of the shadow area under Suzanne?
We want to render out an RGBA image, so first let's determine the opacity i.e. alpha channel of the shadow area. There's no math needed here. We just take the effect that Suzanne has on the ground, invert it, and make it grayscale:
Effect on the ground
Ran through these nodes
Results in this alpha channel
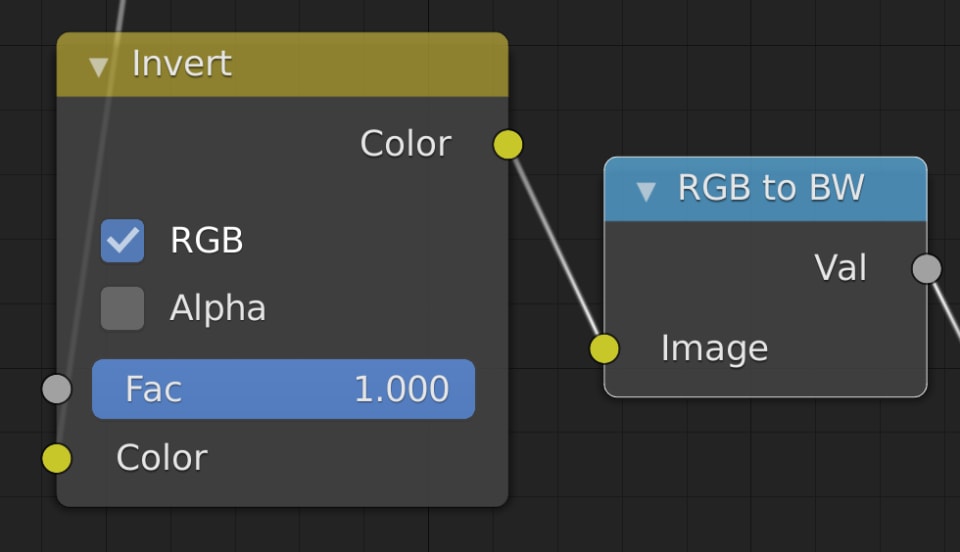
That's a pretty straightforward way of getting the opacity of the shadow area, so we'll work with that.
Now why don't we just use the RGB values of the Suzanne rendered on the ground? These are accurate shadow values right? Yep they are, perfectly accurate in fact. But when we would then lay them on top of a white background using our semitransparent alpha channel, they would be partially mixed with the white background. And that would wash out the colors of the shadow:
The accurate shadow on the left and a very washed out shadow on the right
So that clearly doesn't work if you're after a proper, accurate shadow. Because image compositing is just a bunch of pixel math, let's do a bunch of pixel math.
The math I didn't want to talk about
As promised in the video, we'll finally dive into some math here. (If it's getting too scary, you can scroll down and just download the .blend file, no questions asked)
It's always good to start with what you already know and what you don't know (what to calculate).
Let's look at all the pixel values we already know:
- The final RGB values of the Suzanne image on top of the white background, (I'm going to call this
comp) - The A (alpha) channel of the Suzanne image (let's call this
alpha) - The background color RGB values, white in this case (we'll call this
bg)
And the pixel values we don't (but want to) know:
- The shadow area RGB values of the Suzanne image (it's part of the foreground image so we'll call it
fg)
Remember, this is only about the shadow area of the picture. The RGB values of Suzanne itself, and the distant background, are already known from the rendered image.
So here's first equation. It calculates the composition of an RGBA image onto an RGB background:
What this means, is that the final composite comp is kind of a blend between the foreground fg and the background fg where the alpha channel alpha is used as the blend factor.
If you imagine alpha to be 1.0 , the comp would be 100% of the foreground and 0% of the background. The opposite also works, an alpha of 0.0 would result in 0% of the foreground and 100% of the background. Finally, if you plug in an alpha of 0.5 it would be a 50/50 blend between the foreground and background. Makes sense 👌
Note that I don't distinguish between the different color channels R, G, or B here. This formula works the same way for all three colors.
Now we need to rewrite this equation to be able to calculate our unknown fg pixel values as a function of our known pixel values comp, alpha, and bg.
This is the equation we start with:
Let's subtract (1.0 - alpha) * bg from both sides and switch sides:
And divide everything by alpha to get this equation that calculates the value of fg:
Remember, I was talking about the background being white. So we can actually simplify it a bit. This equation calculates any color channel: R, G, or B. But white has a value of 1.0 for every channel. So when bg = 1.0 we can just get rid of it and end up with:
Which is the same as:
Bam 🤓 That's the final equation to calculate or foreground pixel values.
So now what? How do we translate this into a bunch of compositor nodes?
Turning math equations into compositor nodes
Our first intuition might be to use Math nodes, which could work, but the problem is that Math nodes only apply their magic to a single channel. So if we go that route we'd have to do the same thing three times (for the R, G, and B channels).
If you've watched the video you noticed that I was using Color Mix nodes, these also have some math functionality, enough to cover our equation.
First we start with the part within the brackets:
That looks pretty simple right? Just take the comp, subtract 1.0 and add the alpha channel. We can do that with two Color Mix nodes:
Now there's just one step left: divide by the alpha channel:
And that's all. In the video you see that what comes directly out of these looks quite hideous, but the math is right! 😄Always trust the math.
And when you do, and you plug in the alpha channel with a Set Alpha node. Premultiply it, because that is not done by default with the Set Alpha node, it works pretty great.
Adding Suzanne to our calculated shadow pixels
The steps beyond this are covered in the video. But after we have the proper shadow pixel values, we can simply use an Alpha over node to add the Suzanne render back in. And that gives us the final image we can save to PNG.
Right?
The Colorspace situation
Wrong.. We're not getting off that easy. I have a tendency to not want to think about it and sweep it under the rug, but there's this thing called colorspace...
Everything we've been doing with our ridiculous node chain is composited in linear color space. But a web browser isn't that sophisticated. The browser, and most image formats, all operate in sRGB space.
I talk about it in the video as well, but what it comes down to is that we have to do our math in sRGB space as well to match what's happening in the browser. So to do this conversion, we will use Gamma nodes.
To go from linear to sRGB, we can use a Gamma node with a value of 0.45. This is an approximation, but close enough for a great result. So we first move into sRGB space with a Gamma node set to 0.45. Then after we've done the math and set the alpha channel, we want to transform back to linear. This is because the final Composite node in Blender expects an image input in linear color space. So to go back from sRGB to linear, we use another Gamma node, but now we set the value to 2.2.
Here's the difference between before and after using this color space correction:
Before and after Gamma correction
Now, finally we're there, the math works out, and the image looks good and accurate 🙂
Try it yourself
I hope this made sense. If not, you can still have fun and just use the compositor setup by downloading the .blend file and replacing Suzanne with your own 3D model:
And download the final Suzanne PNG if you want to see it yourself:
What about compressing images for the web?
I did not really cover a fairly important area of rendering images for the web here: Formatting and compressing your images in the most efficient way to show them on your website. The reason I'm not talking about that is because if you run a website and you want to render and export images for it, I highly recommend using an image CDN (content delivery network).
Most CDNs will be able to take care of compressing your images and serving them in the most efficient format, depending on what browser your users are on. They also allow you to serve the same image in different sizes, which is great for serving the smallest possible version for varying screen sizes with varying pixel densities. There are a lot of options for CDNs out there and most of them have a free plan. We are currently using Cloudinary which works quite well.
Also, Johnson has written some more tips about exporting your renders into different formats in this article about exporting images from Blender.